La Cryptologie

Le code de César est la méthode de crytographie par substitution mono-alphabétique la plus ancienne, elle date du Ier siècle avant Jésus Christ et était utilisée par César et ses généraux pour les communications au niveau militaire. "Substitution mono-alphabétique" signifie remplacement d'une lettre par une autre, par décalage de l'alphabet. La faible alphabétisation de la population à cette époque rend cette méthode efficace, mais de nos jours elle ne le serait plus vraiment.

Le fonctionnement de cette méthode est simple, il consiste à décaler les lettres de l'alphabet d'un nombre n qui est la clé.  Par exemple, si on remplace A par C (n=2), on remplace B par D, C par E...

 Exemple: 

Le texte que nous souhaitons coder est le suivant : « décaler les lettres de l'alphabet »,

le texte codé avec une clé n=3 est : « ghfdohu ohv ohwwuhv gh o'doskdehw »

Malheureusement, on comprendra que ce système est très peu sûr, puisqu'il n'y a que 26 lettres dans l'alphabet donc seulement 25 façons de chiffrer un message avec le code de César (on ne peut pas substituer une lettre par elle-même).

Pourtant, son efficace simplicité conduisit les officiers sudistes à le réemployer durant la guerre de Sécession, de même pour l'armée russe qui fit de même durant la première guerre mondiale en 1915.

Le code de César a été utilisé sur des forums internet sous le nom de "ROT13" (rot-ation de 13 lettres c'est-à-dire que: A→N...). Le ROT13 n'a pas pour but de rendre du texte confidentiel et indéchiffrable, mais plutôt d'empêcher la lecture involontaire de celui-ci (par exemple la réponse à une devinette, l'intrigue d'un film, etc.). Pour obtenir le texte en clair, il suffit de re-chiffrer un texte codé en ROT13 une deuxième fois, on revient ainsi à la lettre en clair de départ.

Le codage d'un message grâce à un algorithme qui utilise le code de César :

      Cet algorithme, réalisé par Louis et Maxime, aidés par notre professeur de mathématiques M. Bonzom, permet de coder un message avec une clé choisie que l'on rentre lors du lancement de l'algorithme.

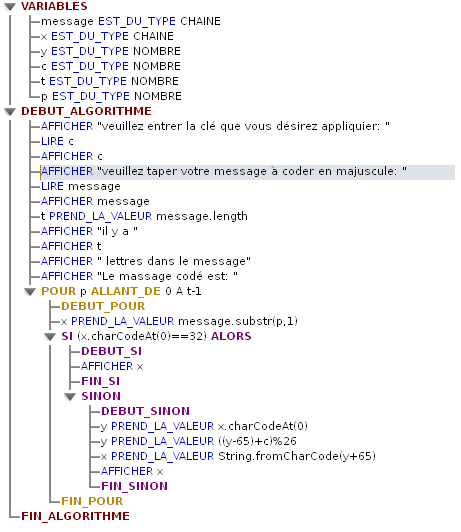
Nous avons tout d'abord déterminé des variables :

-La variable « message » correspond au message à coder

-La variable « x » représente successivement les lettres du message ( une par boucle )

-La variable « c » est la clé choisie par l'utilisateur

-La variable « t » correspond au nombre de lettre dans le message

-La variable « p » représente la position de la lettre dans le message

-La variable « y » est celle qui permet d'appliquer le changement de caractère en utilisant le code ASCII ( le code ASCII d'un caractère correspond à un nombre: par exemple, le code ASCII de la lettre A est 65, et il y a un nombre associé à chaque caractère du clavier d'un ordinateur; ASCII signifie American Standard Code for Information Interchange, c'est une norme de codage utilisée depuis les années 1960 en informatique et pour échanger des informations, et c'est sans doute la plus utilisée encore aujourd'hui).

Puis, nous avons demandé à l'utilisateur de l'algorithme de rentrer la clé qu'il souhaite utiliser ( la variable « c ») ainsi que le message qu'il souhaite coder en majuscule ( la variable « message » ). Ensuite, à partir du message, la variable « t » intervient et donne le nombre de caractères contenus dans le message grâce à la formule : message.lenght. Par la suite, nous avons créé une boucle « pour...allant de...à... » avec la variable « p » qui va du premier caractère (à qui on associe le chiffre 0) au dernier caractère (qui prend la valeur  t-1, soit le dernier caractère du message). Cette boucle sera donc répétée autant de fois qu'il y a de caractères dans le message. Dans cette boucle, si le caractère est un espace, aucun changement n'est appliqué à celui-ci ; dans le cas contraire, on applique au caractère la clé en s'aidant du code ASCII. Suite à la première étape, « y » a la valeur du code ASCII du caractère analysé dans cette boucle. La deuxième étape consiste à appliquer le changement opéré par la clé sur le caractère. «%26 » équivaut à « modulo 26 », ce qui revient à diviser par 26 et à prendre le reste de la division euclidienne. Cela permet de créer une boucle: à la suite du Z on retrouve le A puis l'alphabet continue ( par exemple si le caractère est Y et qu'on lui applique un décalage de 3, le nombre associé sera 28, on le divise par 26 et le reste est 2, la lettre Y devient donc la lettre B). Pour finir, la dernière étape permet de retranscrire le nombre obtenu en une lettre à partir du code ASCII.

Enfin, le message codé s'affiche par la répétition des boucles.

Le code ASCII de la barre espace :

     Lors de la réalisation de l'algorithme permettant de coder un message avec le codage César, nous avons rencontré un problème. Lorsqu'il y avait un ou plusieurs espaces dans le message à coder, ces espaces étaient transformés en d'autres caractères tels que le point d'interrogation, le point virgule, l'étoile, la virgule... en fonction de la clé utilisée. Pour remédier à ce problème, nous avons créé l'algorithme ci-dessous permettant de déterminer le code ASCII du caractère "espace".

Dans cet algorithme, la variable « message » est le message, la variable « x » est le premier caractère de ce message, puis la variable « y » est le code ASCII de ce caractère.

Cela nous a donc permis de connaître le code ASCII du caractère "espace": il est égal à 32.

Le décodage d'un message grâce à un algorithme utilisant le code de César :

     L'Algorithme ci-dessous a été réalisé par Maxime et Louis.

     Nous nous sommes inspirés de l'algorithme précédent qui permet de coder un message donné. Une fois le message codé obtenu, nous l'avons écrit puis nous l'avons rentré dans ce nouvel  algorithme, pour le décoder et observer s'il s'agit bien du message entré précédemment.

     Encore une fois, nous avons tout d'abord déclaré les variables :

-La variable « message » est le message à décoder

-La variable « x » représente successivement les lettres du message ( une par boucle )

-La variable « c » est la clé qui ici est inconnue

-La variable « t » correspond au nombre de lettres dans le message

-La variable « p » représente la position de la lettre dans le message

- Et la variable « y » est celle qui permet d'appliquer le changement de caractère en utilisant le code ASCII

Puis, nous avons demandé à l'utilisateur de l'algorithme de rentrer le message qu'il souhaite décoder ( la variable « message »). Ensuite, à partir de ce message, la variable « t » intervient et donne le nombre de caractères contenus dans le message grâce à la formule : message.lenght. Par la suite, nous avons créé une première boucle pour la clé, qui se répète 25 fois pour tester toutes les possibilités de décalage ayant été opéré par la clé qui nous est inconnue. Puis, dans cette boucle, nous avons inséré la boucle qui nous avait permis de coder un message dans l'algorithme précédent.

Lorsqu'on le lance, cet algorithme nous donne donc 25 possibilités de décalage et une de celles-ci est le message initial. Nous avons eu des difficultés avec l'affichage final de l'algorithme qui mettait soit les possibilités toutes à la suite sur une grande ligne, soit lettre par lettre en descendant. 

Mais nous avons réussi à remédier à ce problème en affichant un message contenant uniquement un espace pour pouvoir y ajouter un « retour à la ligne »,  afin que les solutions s'affichent de la manière suivante qui est nettement plus lisible et claire.

Les fréquences d'Al Kindi :

Abu Youssouf Ya'qûd Ibn Ishâq Al-Kindi (plus connu sous le nom d'Al-Kindi) était surnommé le « philosophe des Arabes », il s'est penché sur de nombreux sujets différents et a rédigé de nombreux écrits sur ses travaux mais malheureusement ceux-ci ont disparu.

Parmi tous ces travaux, il a développé une méthode de cryptanalyse ( décryptage ) permettant de décoder le codage de César et tous les codages par substitution mono-alphabétique, en utilisant la fréquence moyenne d'apparition de chaque lettre de l'alphabet dans la langue française :

 Nous pouvons ensuite comparer les fréquences obtenues dans le texte avec les fréquences ci-dessus, par exemple sachant que le E est la lettre  la plus courante, on regarde quelle lettre est la plus courante dans un message crypté et on en déduit que dans le message en clair cette lettre sera le E. On fait de même avec toutes les lettres, pour au final remplir le tableau des fréquences dans le texte à analyser et attribuer à chaque lettre codée la lettre décodée correspondant à la même fréquence dans la langue française en général.

Cette méthode de déchiffrement par comparaison est particulièrement efficace pour des messages d'une longueur assez importante, mais pour un message très bref les fréquences d'apparition des lettres ne seront pas forcément représentatives. Par exemple si le message est simplement : « BONJOUR » on n'a aucune apparition de la lettre E alors que celle-ci est censée être la plus fréquente, et il y a la lettre J alors qu'elle n'a que 0,89% de chance d'apparaitre en moyenne.

Nous avons ensuite expérimenté cette méthode à l'aide du tableur: 

 Dans le fichier tableur ci-dessus, on inscrit le message à analyser dans la colonne B et on l'inscrit dans autant de lignes que de caractères dans le message. Dans la colonne C, on utilise une formule que permet d'inscrire en C1 le premier caractère du message, puis en C2 les deux premiers caractères du message, puis en C3 les trois premiers caractères du message, et ainsi de suite.. On a ensuite utilisé dans la colonne D, une formule qui inscrit dans la cellule uniquement le caractère le plus à droite parmi ceux de la cellule de la colonne C se trouvant sur la même ligne. On a donc dans la colonne D le message inscrit verticalement.

 On a ensuite utilisé dans le tableau ci-dessus une formule permettant d'analyser le nombre de fois qu'apparaît chaque lettre dans le message à décoder. On peut donc ensuite retranscrire ces nombres sous forme de fréquence en pourcentage, remplir le tableau de fréquences, puis le comparer à celui des lettres dans la langue française pour finalement décoder le message. 

Cette méthode, bien qu'efficace, est tout de même longue et fastidieuse. Il est donc vraiment plus rapide de décoder un message à l'aide de notre algorithme de décodage.

 Page suivante